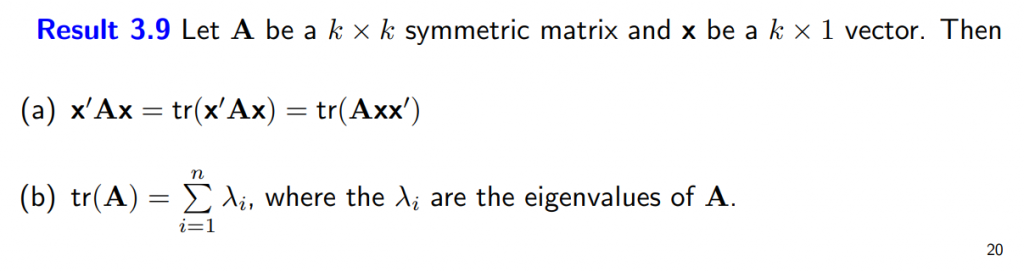LDA （Linear Discriminant Analysis）

LDA 與 QDA 模型建立的出發點相同，都是以群組的後驗機率的大小，如下式，決定資料所在群組。因為後驗機率在計算上有困難，或是說在大多數的情境下，直接依照後驗機率的定義是無法計算。所以，須先將後驗機率轉換為先驗機率的問題。之後，經過一些數學上的推導，計算使後驗機率最大的群組 k。

首先，由貝氏定理，後驗機率

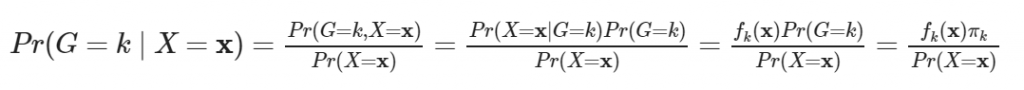
為先驗機率 Pr(G=k) 的函數。

LDA Assumption: multivariate normal with homogeneous variance-covariance matrices

LDA 假設：

其中，k 表第 k 群的資料。同理，μk 為第 k 群的母體均數向量。另外，Σ > 0。
所以，資料 X 所屬群組 G 的 PDF 為

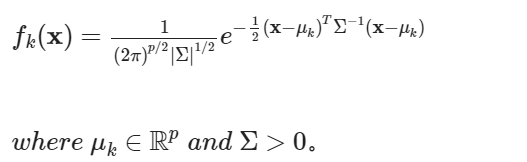
將上式與代入後驗機率的式子，得到

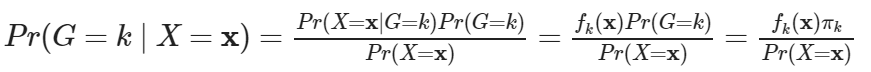
將等式兩側同時取自然對數，則

LDA 之判定函數（discriminant function）

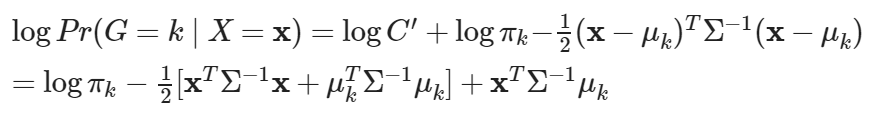
為求所在之群組

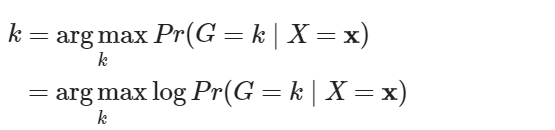
其中

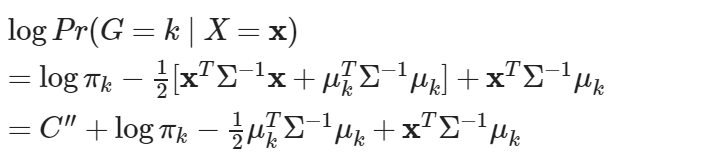
以判斷資料所屬之群組。

決策邊界（Decision boundary / Decision surface）

LDA 的群組分界線是如何畫出來的呢？理論的關鍵在於找出群組間的共同條件，在此為後驗機率。以 2 個群組間分群為例，在給定的資料下，設群組 k 與群組 l 的後驗機率相等，則決策邊界發生在 δk = δl，即

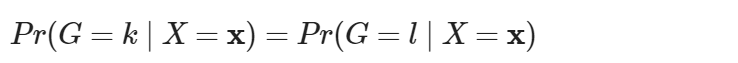
為群組 k、群組 l 間的決策邊界。

參考資料

1. LDA 數學推導過程
   （Google 關鍵字： LDA MULTIVARIATE NORMAL）

• Stanford University - STATS 202: Linear Discriminant Analysis (LDA)
• Penn State University - STAT 505 Applied Multivariate Statistical Analysis: Lesson 10: Discriminant Analysis

2. 線性代數

• Trace：Wiki Trace (linear algebra)-Properties of Trace
• 內積： Wiki 內積-性質
• 二次式之 Trace 特性: The Multivariate Normal Distribution 簡報第20頁, 其中重點如下圖。
• 二次式之 Trace 與偏微分 CHAPTER 13. THE MULTIVARIATE GAUSSIAN, page 8.